
Zadanie Wiarygodność świadków (wia)
Pomóż nam usprawnić bazę zadań!
Wiarygodność świadków
Limit pamięci: 32 MB
Sąd dysponuje zeznaniami świadków oznaczonych kolejno liczbami naturalnymi 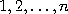 .
Każde zeznanie jest stwierdzeniem postaci: „świadek
.
Każde zeznanie jest stwierdzeniem postaci: „świadek 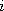 zgadza się ze świadkiem
zgadza się ze świadkiem 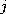 ” albo „świadek
” albo „świadek 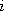 nie zgadza się ze świadkiem
nie zgadza się ze świadkiem 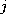 ”.
”.
Jeśli świadek 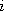 zgadza się ze świadkiem
zgadza się ze świadkiem 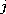 , oznacza to, że świadek
, oznacza to, że świadek 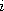 zgadza się też ze wszystkimi świadkami,
z którymi zgadza się świadek
zgadza się też ze wszystkimi świadkami,
z którymi zgadza się świadek 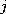 oraz nie zgadza się ze wszystkimi świadkami, z którymi nie zgadza się świadek
oraz nie zgadza się ze wszystkimi świadkami, z którymi nie zgadza się świadek 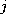 .
Przyjmuje się przez domniemanie, że każdy świadek stwierdza: „Zgadzam się ze sobą”.
.
Przyjmuje się przez domniemanie, że każdy świadek stwierdza: „Zgadzam się ze sobą”.
Mówimy, że świadek nie jest wiarygodny, jeśli z zeznań świadków, będących w posiadaniu sądu wynika, że jednocześnie zgadza się on i nie zgadza z pewnym dowolnym świadkiem.
Zadanie
Napisz program, który:
- wczytuje ze standardowego wejścia liczbę świadków i ich zeznania,
- znajduje wszystkich świadków, którzy nie są wiarygodni,
- zapisuje wynik na standardowe wyjście.
Wejście
W pierwszym wierszu standardowego wejścia jest zapisana jedna liczba całkowita  ,
spełniająca nierówności
,
spełniająca nierówności 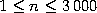 .
Jest to liczba świadków.
W drugim wierszu jest zapisana jedna liczba całkowita
.
Jest to liczba świadków.
W drugim wierszu jest zapisana jedna liczba całkowita 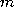 , spełniająca nierówności
, spełniająca nierówności 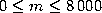 .
Jest to liczba zeznań.
.
Jest to liczba zeznań.
W każdym z kolejnych 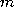 wierszy jest zapisana para liczb całkowitych
wierszy jest zapisana para liczb całkowitych 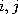 , oddzielonych pojedynczym odstępem,
gdzie
, oddzielonych pojedynczym odstępem,
gdzie 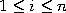 ,
, 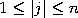 .
Jeśli liczba
.
Jeśli liczba 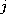 jest dodatnia — jest to zapis zeznania: „świadek
jest dodatnia — jest to zapis zeznania: „świadek 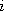 zgadza się ze świadkiem
zgadza się ze świadkiem 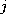 ”.
Jeśli liczba
”.
Jeśli liczba 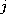 jest ujemna — jest to zapis zeznania: „świadek
jest ujemna — jest to zapis zeznania: „świadek 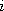 nie zgadza się ze świadkiem
nie zgadza się ze świadkiem  ”.
”.
Wyjście
Na standardowe wyjście należy zapisać:
- jedno słowo NIKT, jeśli na podstawie zeznań nie można znaleźć żadnego świadka, który nie jest wiarygodny,
- albo — w porządku rosnącym — numery świadków, którzy nie są wiarygodni.
Przykład
Dla danych wejściowych:
6 12 1 3 1 6 2 -1 3 4 4 1 4 -2 4 5 5 -1 5 -3 5 2 6 5 6 4
poprawną odpowiedzią jest:
1 3 4 6
Autor zadania: Grzegorz Jakacki.
Kontakt
In the event of technical difficulties with Szkopuł, please contact us via email at [email protected].
If you would like to talk about tasks, solutions or technical problems, please visit our Discord servers. They are moderated by the community, but members of the support team are also active there.

 English
English